Yang-Le Wu

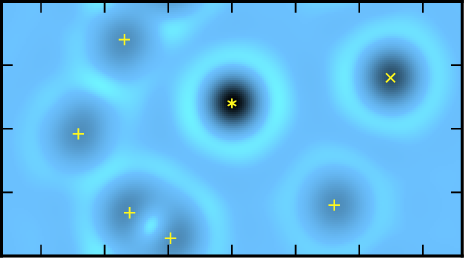
Non-Abelian anyons are among the most striking manifestations of topological order. These exotic excitations have been at the center of a huge research effort in recent years, partly driven by the possibility of constructing topologically fault-tolerant quantum computers. In this context, of particular importance are the Fibonacci anyons. They provide a representation of the braid group rich enough to carry out universal quantum computations, which cannot be achieved with simpler non-Abelian anyons such as the Majorana fermions.

It had long been conjectured that the quasiholes in the ℤ₃ Read-Rezayi state, which may describe the filling ν = 12/5 fractional quantum Hall plateau, are Fibonacci anyons when sufficiently separated. However, this conjecture had not been supported by any microscopic evidence, due to the sheer complexity of the ℤ₃ Read-Rezayi quasihole wave functions. In fact, beyond the conjectured universal topological properties, very little was known about these elusive excitations.

braiding non-Abelian quasiholes

In Phys. Rev. Lett. 113, 116801, we settled this long-standing problem and explicitly demonstrated the Fibonacci nature of the ℤ₃ Read-Rezayi quasiholes. 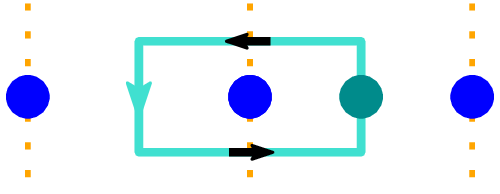Through a numerical study of the model wave functions, we established the exponential convergence of the braiding matrices with increasing quasihole separations, and we extracted the associated length scales as well as the quasihole radii. This puts an upper bound on the desirable quasihole density in interferometer devices — at a higher density, the ℤ₃ Read-Rezayi quasiholes exhibit clear non-universal deviations from the Fibonacci anyons.

In addition, we also provided a microscopic diagnosis for the pathology of the Gaffnian wave function, which was conjectured not to give rise to sensible braiding statistics due to its root in non-unitary conformal field theories. We explicitly demonstrated that the non-universal, path-dependent contributions to the braiding matrices follow a power-law rather than exponential decay as quasihole separations increase. This signals the failure of plasma screening and highlights the gapless nature of the Gaffnian. Our results largely ruled out the possibility of salvaging this pathological wave function as the description of a gapped phase with topological order.

matrix product state description of fractional quantum Hall effect

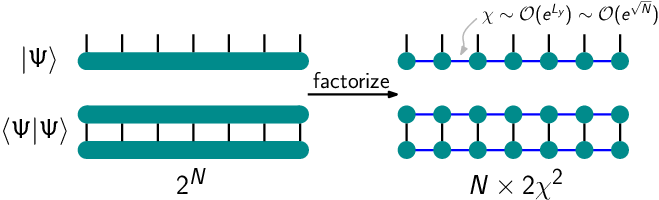
The above progress was enabled by the recent breakthrough of the exact matrix product states for fractional quantum Hall effect. Essentially, the matrix product state is a factorization of the many-body wave function. This factorization makes it possible to exploit the entanglement area law and to store quantum information compactly, and it also greatly facilitates the calculation of physical observables. Its appearance in the quantum Hall context is deeply rooted in the bulk-edge correspondence. Namely, a large class of quantum Hall trial states are described by many-point correlation functions in chiral conformal field theories (CFT). Each electron / quasihole in the quantum Hall wave function is represented by a primary field operator in the conformal correlator. Since a field operator is essentially an infinite-dimensional matrix over the CFT Hilbert space, the conformal correlator, and thus the quantum Hall trial state, can be cast in the form of a matrix product state (MPS). After a truncation of descendants in the CFT Hilbert space, a field operator (or more precisely, the corresponding 3-point function in the CFT) can be well approximated by a finite-size (albeit large) matrix. Such matrices can be constructed numerically from the Virasoro algebra, even for interacting CFTs.

This provides an extremely powerful numerical tool to study the strongly-correlated physics in fractional quantum Hall phases. For our purposes, the MPS technique enables a brute-force evaluation of the conformal-block wave functions with an arbitrary number of quasiholes, without relying on bosonization tricks. It grants access to much larger system sizes than previously attainable, and opens an avenue to the direct characterization of physical properties without confronting the exponentially large many-electron Hilbert space. In Phys. Rev. B 92, 045109, we provided a pedagogical description of the MPS construction. In particular, we discussed in detail how to build MPS for non-Abelian quasiholes with conformal-block normalization and monodromy.

Stabilizing non-Abelian fractional quantum Hall states often requires careful softening of the Coulomb repulsion between electrons. In realistic setups, this task can be extremely challenging. One possible avenue for highly tunable interactions comes from multi-component quantum Hall systems, such as bilayers or wide quantum wells. These systems typically feature a rich variety of topological phases and interaction-driven topological phase transitions. Unfortunately, the internal degrees of freedom that provide tunability also impose a heavy burden on microscopic numerical calculations. As a result, many such systems have not been thoroughly explored.

In Phys. Rev. B 92, 035103, we initiated a systematic numerical study of quantum Hall bilayers at filling ν = 2/3. Using a combination of exact diagonalization and variational Monte Carlo, we mapped out the phase diagram in both the lowest and the second Landau levels as a function of interlayer separation and tunneling strength. We found that the ℤ₄ Read-Rezayi state is highly competitive in the second Landau level.

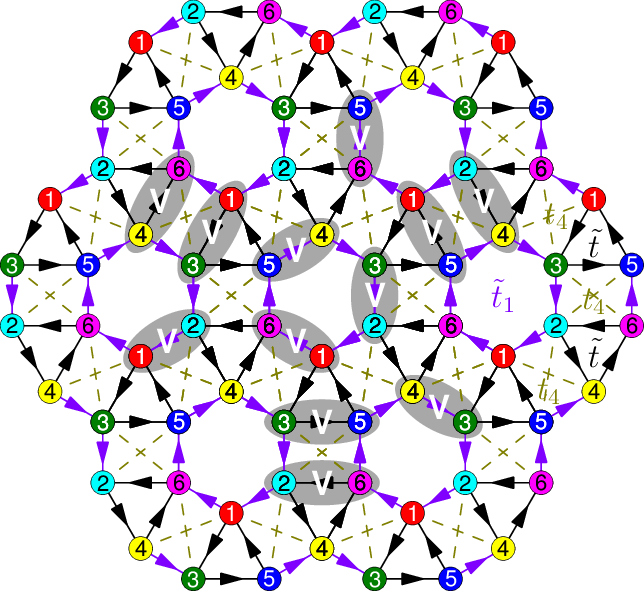
Interactions can stabilize strongly-correlated phases in topological flat bands with nonzero Chern number C. These so-called fractional Chern insulators (FCI) exhibit fractional quantum Hall effect at zero magnetic field. In Phys. Rev. B 85, 075116, using exact diagonalization and particle entanglement spectrum, we demonstrated numerically the existence of the FCI phase in an array of lattice models with a C = 1 flat band. This includes both Abelian and non-Abelian quantum Hall states. We found a correlation between the stability of the strongly-correlated phase and the uniformity of the Berry curvature in the band structure.

The nature of the FCI ground state at C = 1 can be understood by the Wannier mapping between a Chern band and the lowest Landau level (LLL). In Phys. Rev. B 86, 085129, after a proper gauge fixing, we transcribed the continuum Laughlin state to the lattice, and achieved high overlaps with the FCI ground state.

For FCI with C > 1, however, numerical studies revealed anomalous features distinct from the usual multicomponent quantum Hall states. In Phys. Rev. Lett. 110, 106802, we found that the correct one-body mapping for C > 1 involves a specially crafted set of boundary conditions for the multicomponent LLL. This new boundary condition sews together the C components into a single manifold with Chern number C. Using the modified one-body mapping, we constructed pseudopotential Hamiltonians and model wave functions for FCI with an arbitrary Chern number. Our model wave functions correctly capture the subtle differences between the lattice FCI states and the usual multicomponent quantum Hall states. In Phys. Rev. B 89, 155113, we analyzed the FCI pseudopotential Hamiltonian in the thin-torus limit. This revealed a generalized Pauli principle for the degeneracy of the FCI ground states in each Bloch momentum sector. A reference implementation of the corresponding counting rule is available here.

In the past, I have also studied the pairing mechanism of iron-selenide superconductor using functional renormalization group.

Before coming to the US for graduate school, I worked with Professor Qi Ouyang as an undergraduate Chun-Tsung Scholar at Peking University, on the origin of the dynamical robustness of regulatory networks in living cells, and on the non-linear dynamics of reaction-diffusion systems.